# LZW压缩
# 摘要
- 是一种数据压缩算法
- 可以处理变长模式,最终生成一张定长的编码编译表
- 生成编译表的过程在压缩过程中完成,而不是先生成完整编译表再压缩
- 输出数据时不用附上编译表
# 1 背景
LZW压缩算法,全称为“Lempel-Ziv-Welch Encoding”,是Unisys的专利,在2003后失效,可随意使用。
# 2 LZW算法思想
我们知道每一个字符通常是使用ASCII码来表示的,这样每个字符占7位。
如果有文本:A B C A B C A B C ...
不难看出文本中含有大量重复子字符串ABC。如果我们可以将这样重复的子字符串统一编码,便可以对文本进行压缩。不仅如此,如果可以读取到更长的重复子串(ABCABC...),则可以大幅缩短压缩空间。
# 3 LZW的单词查找树
由于重复字符串可能存在大量相同的前缀,我们使用线性表来保存编译表显然会浪费很多不必要的空间。因此使用单词查找树来表示编译表是一种不错的方法。
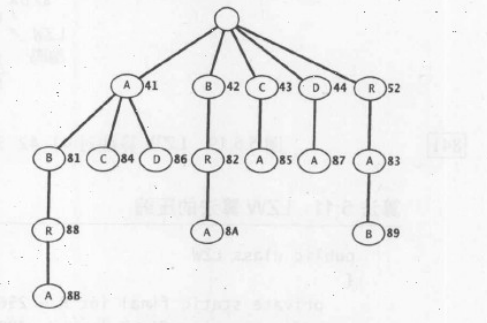
# 4 算法实现
算法实现包含两个方法,compress()和expand()。
# 4.1 压缩过程
压缩过程如下:
- 初始化一个空的编译表
- 在每次读取过程,重复以下步骤:
- 找出未处理的输入在编译表中最长的前缀字符串s;
- 输出s的编码值
- 继续扫描s之后的下一个字符c;
- 在符号表中将s+c(字符串连接)的值设为下一个编码值。

public class LZW {
private static final int R = 256; // 输入字符数
private static final int L = 4096; // 编码总数 = 2^12
private static final int W = 12; // 编码宽度
public static void compress() {
String input = BinaryStdIn.readString();
TST<Integer> st = new TST<Integer>();
for (int i = 0; i < R; i++) {
st.put("" + (char) i, i);
}
int code = R + 1; // R为文件结束(EOF)的编码
while (input.length() > 0) {
String s = st.longestPrefixOf(input); // 找到匹配的最长前缀
BinaryStdOut.write(st.get(s), W); // 打印出s的编码
int t = s.length();
if (t < input.length() && code < L) // 将s加入符号表
st.put(input.substring(0, t + 1), code++);
input = input.substring(t); // 从输出中读取s
}
BinaryStdOut.write(R, W); // 写入文件结束符标记
BinaryStdOut.close();
}
}
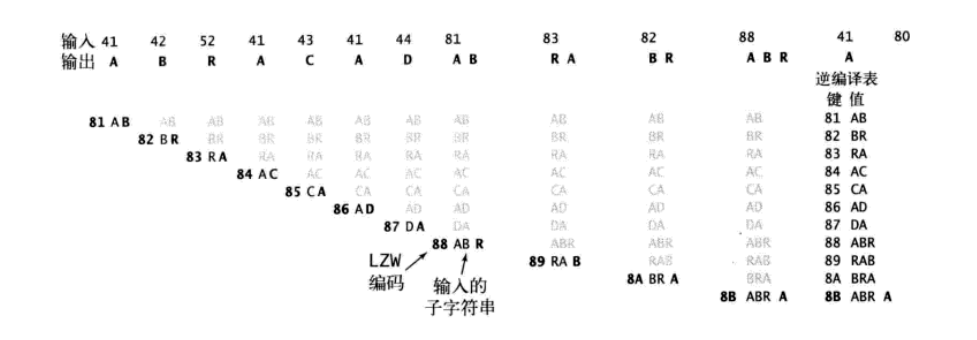
# 4.2 展开过程
展开过程如下:(编译表为编码值x和对应字符串s的映射)
- 先读取输入中的下一个编码x,第一个编码必可以翻译为一个对应的字符s的ASCII码。
- 将val设为s
- 重复以下步骤:
- 输出val
- 从输入中读取下一个编码x
- 在编译表中将s设为和x相关联的值
- 在编译表中将下一个未分配的编码值设为val+c(字符串连接),其中c为s的首字母
- 将当前字符串val设为s
public class LZW {
private static final int R = 256; // 输入字符数
private static final int L = 4096; // 编码总数 = 2^12
private static final int W = 12; // 编码宽度
public static void expand() {
String st = new String[L];
int i;
for (i = 0; i < R; i++) { // 用字符初始化编译表
st[i] = "" + (char) i;
}
int codeword = BinaryStdIn.readInt(W);
String val = st[codeword];
while (true) {
BinaryStdOut.write(val); // 输出当前子字符串
codeword = BinaryStdIn.readInt(W);
if (codeword == R) break;
String s = st[codeword]; // 获取下一个编码
if (i == codeword) // 如果前瞻字符不可用(这步请参考下文特殊情况的解决)
s = val + val.charAt(0); // 根据上一个字符串的首字母得到编码的字符串
if (i < L)
st[i++] = val + s.charAt(0); // 为编译表添加新的条目
val = s; // 更新当前编码
}
BinaryStdOut.close();
st[i++] = " "; // (未使用)文件结束标记(EOF)的前瞻字符
}
}
# 4.3 特殊情况的解决
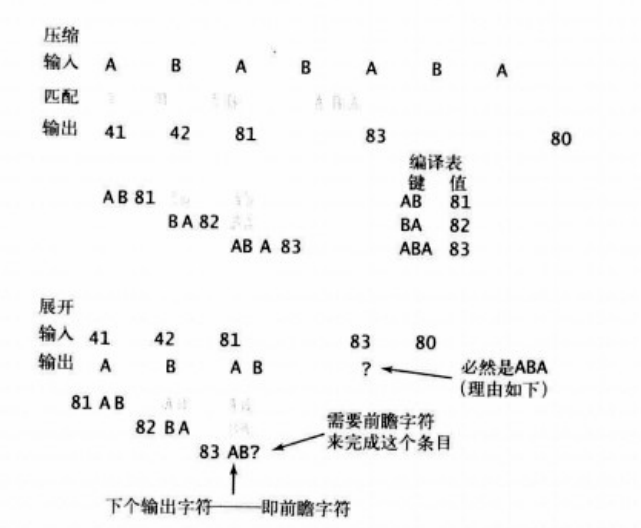
想象一下这种情况:ABABABA
根据我们以上的算法,算法步骤如下:(假设从80开始编码)
- 对A编码,41,前瞻B,拼得为AB,81加入编译表
- 对B编码,42,前瞻A,拼得为BA,82加入编译表
- 对AB编码,81,前瞻A,拼得为ABA,83加入编译表
- 对ABA编码,83,结束并再输出80(EOF)
总结下压缩后的输出为41 42 81 83 80。
展开时,根据我们的算法有这个问题:
- 读41,输出A,并读42得到前瞻字符B,将AB,81加入编译表
- 读42,输出B,读取81,得到前瞻A,将BA,82加入编译表
- 读81,输出AB,读取83,编译表中没有83。出现问题。
- 读83,编译表中没有83。错误
显然我们发现问题的原因是,81(AB)恰好是83(ABA)的前缀,但由于ABA的出现,在压缩时使用了83而非81 41。
这种情况的解决方法是,如果遇到编译表中不存在的条目,前瞻字符必须是当前输出字符串的首字母。
因此第3、4步解决方法为:
- 读81,输出AB,读取83,编译表中没有83,前瞻为当前AB的首字母A,将ABA,83加入编译表。
- 读83,输出ABA,读取80,为EOF,结束。
← 霍夫曼压缩