Jinze Song's Blog

# 霍夫曼压缩

# 摘要

  • 是一种数据压缩算法
  • 使用变长前缀码
  • 需要额外的空间（如构造单词查找树）来生成编码编译表
  • 为输入中的定长模式产生一种变长的编码编译表
  • 输出压缩后的数据时，需要同时输出编码编译表
  • 算法本质是寻找最优前缀码

# 1 背景

霍夫曼压缩是一种字符串压缩算法，可以大幅压缩自然语言文件空间。这种寻找最有前缀码的通用方法是D.Huffman再1952年发现的，因此被称为霍夫曼编码。

# 2 变长前缀码

# 2.1 为什么需要变长前缀码？

比如有一段文本(十亿个单词，只有ABC) ；A B C A C A B ... 通常来说我们在机器中可以直接使用ASCII码来保存这段字符串，但问题是每个ASCII码需要7位二进制来存储，而文本的字典大小（ABC）显然不太需要7位这么长的格式。由此我们引出了变长前缀码。
使用变长前缀码需要注意，每个字符的编码不能是另一个字符的前缀。
比如我们将A设为1，B设为01，C设为001。这种构建方法不唯一。

# 2.2 前缀码的单词查找树

表示前缀码，最简单的方法是使用单词查找树。在这里不赘述单词查找树的基本概念（可搜索单词查找树相关博文）

  • 叶节点储存字典中的字符
  • 解码过程中，0表示向左节点，1表示向右节点。

# 2.3 最优前缀码

在2.1中我们提到，构建前缀码的结果不唯一，压缩率也不唯一。但我们可以通过霍夫曼编码找到最优前缀码。这种前缀码的特点为：

  • 在文本中出现的频率越多的字符，编码的位数越小。
  • 最优前缀码表示法唯一。
  • 任何一种文本，都能找到最优前缀码。

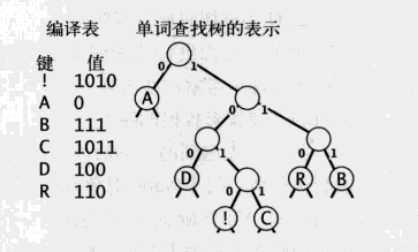
霍夫曼编码

# 3 构建霍夫曼编码的单词查找树

单词查找树的节点表示

private static class Node implements Comparable<Node>{
    // 霍夫曼单词查找树中的节点
    private char ch;   //如果是叶节点，表示字符
    private int freq;  //当前节点下所有叶节点表示的字符频率和
    private final Node left, right;
    
    Node(char ch, int freq, Node left, Node right){
        this.ch     = ch;
        this.freq   = freq;
        this.left   = left;
        this.right  = right;
    }

    public boolean isLeaf(){
        return left == null && right == null;
    }

    public int compareTo(Node that){
        return this.freq - that.freq;
    }
}

# 3.1 构建

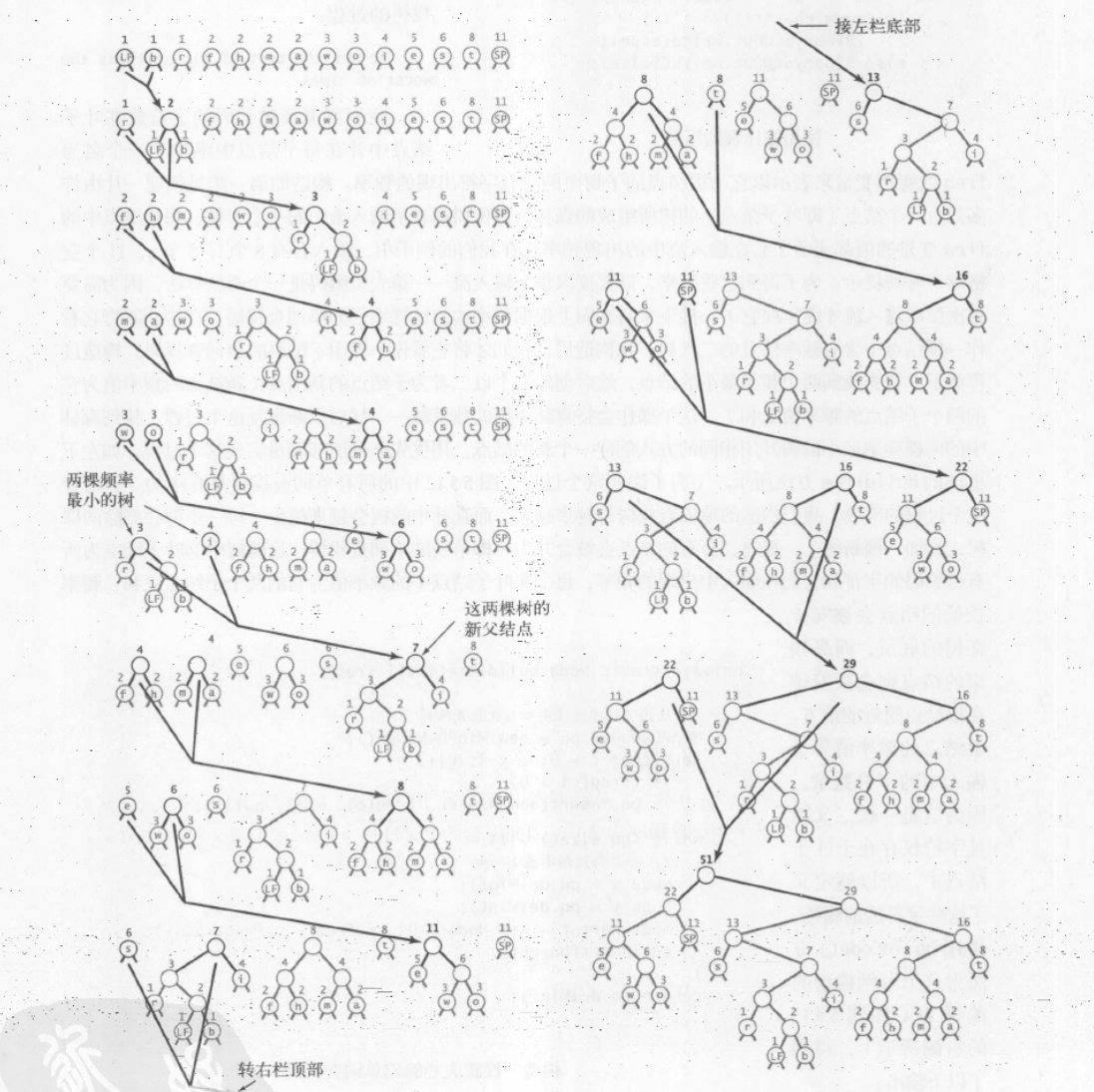
构建单词查找树

# 3.2 输出为比特流

public static void writeTrie(Node x){
    if(x.isLeaf()){
        BinaryStdOut.write(true);
        BinaryStdOut.write(x.ch);
        return;
    }
    BinaryStdOut.write(false);
    writeTrie(x.left);
    writeTrie(x.right);
}

# 3.3 从比特流中读取

private static Node readTrie(){
    if(BinaryStdIn.readBoolean())
        return new Node(BinaryStdIn.readChar(), 0, null, null);
    return new Node('\0', 0, readTrie(), readTrie());
}

# 4 霍夫曼压缩算法实现

压缩方法：

  1. 读取输入
  2. 统计输入中的每个字符的出现频率
  3. 根据频率构造霍夫曼编码树
  4. 根据霍夫曼编码树构造编译表
  5. 根据编译表压缩文本（将文本翻译为压缩后的格式）
  6. 输出单词查找树（可编码为比特流）、文本字符总量、压缩后的文本

展开方法：

  1. 读取单词查找树
  2. 读取需要解码的字符数量
  3. 使用单词查找树将比特流解码
public class Huffman{
    private static int R = 256;  //ASCII字母表

    public static void compress(){
        // 读取输入
        String s = BinaryStdIn.readString();
        char[] input = s.toCharArray();
        // 统计频率
        int[] freq = new int[R];
        for(int i = 0; i < input; i++){
            freq[input[i]]++;
        }
        // 构建霍夫曼编码树
        Node root = buildTrie(freq);
        // (递归地) 构造编译表
        String[] st = new String[R];
        buildCode(st, root, "");
        //(递归地) 打印解码用的单词查找树
        writeTrie(root);
        // 打印字符总数
        BinaryStdOut.write(input.length());

        // 使用霍夫曼编码处理输入
        for(int  i = 0; i < input.length; i++){
            String code = st[input[i]];
            for(int j = 0; j < code.length(); j++){
                if(code.charAt(j) == "1"){
                    BinaryStdOut.write(true);
                }
                else BinaryStdOut.write(false);
            }
        }
        BinaryStdOut.close();
    }
}

← LZW压缩 →