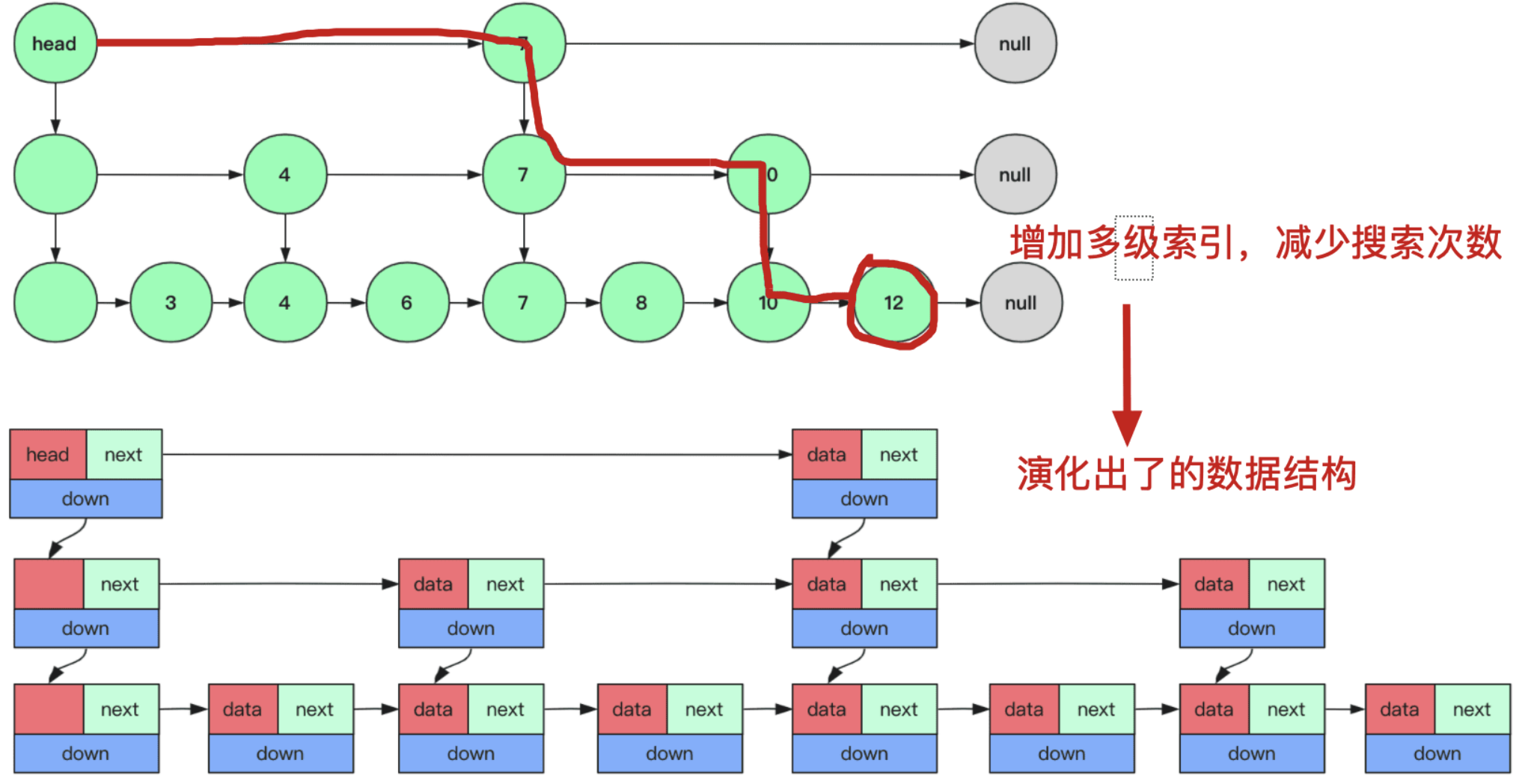
数据结构

每个元素记录

// src/server.h

/* ZSETs use a specialized version of Skiplists */
typedef struct zskiplistNode {
    sds ele;
    double score;
    struct zskiplistNode *backward;
    struct zskiplistLevel {
        struct zskiplistNode *forward;
        unsigned int span;
    } level[];
} zskiplistNode;

typedef struct zskiplist {
    struct zskiplistNode *header, *tail;
    unsigned long length;
    int level;
} zskiplist;

其中最重要的就是backward和level。

• backward可以理解为每一个node的上一个。
• level可以理解为当前层级以及所有下层。span表示当前层中当前node和下一个node forward的距离。

例如一个跳表：

level1: 1 2 3 4 5;
level2: 1 3 5
level3: 1 5

我们对于3这个node，他属于level2和level1，那么其level[]就包含两层，其中
level2: 3 -> span=1 forward=5
level1: 3 -> span=0 forward=4 -> span=0 forward=5

查找

跳表的高度是lg(n)，查找复杂度为lg(n)

增加和删除

增加的时候对于每个增加的元素，计算其level的概率。我们假设整个跳表按照2的次方来计算索引，那么可以认为每一个level 概率p为1/2。

那么理解为每一个新增的node依次向上进行level p概率“晋升”。level 1 p=1，level 2 p=1/2，level 3 p=1/2 * 1/2=1/4 等。

redis中的实现如下：

其中random()是随机数，而ZSKIPLIST_P就是晋升概率，可以自己设置。如果晋升概率小，则整体空间利用率会比较高，但是查找的性能会下降。

// src/t_zset.c

/* Returns a random level for the new skiplist node we are going to create.
 * The return value of this function is between 1 and ZSKIPLIST_MAXLEVEL
 * (both inclusive), with a powerlaw-alike distribution where higher
 * levels are less likely to be returned. */
int zslRandomLevel(void) {
    int level = 1;
    while ((random()&0xFFFF) < (ZSKIPLIST_P * 0xFFFF))
        level += 1;
    return (level<ZSKIPLIST_MAXLEVEL) ? level : ZSKIPLIST_MAXLEVEL;
}

跳表的高度是lg(n)，因此复杂度都是lg(n)。